Closely Examining the Distribution of Scores on a Recent Test: Key Insights
- Understanding the distribution of scores on a recent test closely: what it reveals
- How to analyze the distribution of scores on a recent test closely — step-by-step methods
- Visualizing the distribution of scores on a recent test closely: histograms, box plots, and density curves
- Key statistics to extract from the distribution of scores on a recent test closely (mean, median, variance, skewness)
- Interpreting anomalies and turning the distribution of scores on a recent test closely into actionable insights
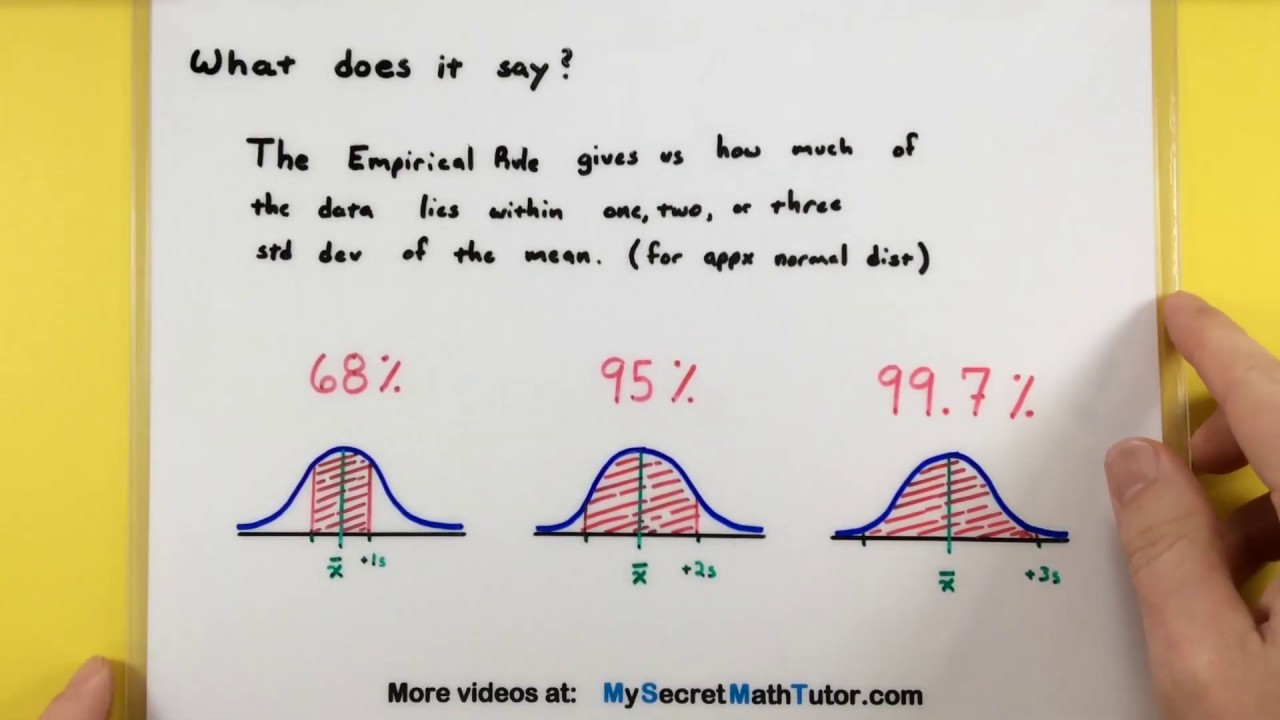
Understanding the distribution of scores on a recent test closely: what it reveals
Examining the distribution of scores on a recent test reveals more than average performance; it highlights patterns in learning and assessment quality. A closely inspected score distribution shows central tendencies like the mean and median that indicate typical performance, while also exposing the spread (variance and standard deviation) that signals whether most students performed similarly or whether results vary widely. Identifying whether the distribution is clustered, uniform, or widely dispersed helps educators understand if the test effectively differentiated student mastery.
Skewness and the presence of outliers in the score distribution point to specific instructional or test-design issues. A left or right skew can suggest that items were too easy or too difficult overall, while outliers may indicate misadministration, cheating, or individual learning challenges. Paying attention to these features supports targeted item analysis to determine which questions disproportionately influenced the distribution and where content or scaffolding adjustments are needed.
Analyzing subgroups within the distribution—by class section, demographic group, or prior achievement level—can uncover performance gaps that the overall average masks. When subgroup score distributions diverge, it signals equity concerns or differential item functioning, prompting educators to review curriculum alignment, access to resources, or culturally responsive teaching practices. Using visual tools like histograms or kernel density plots alongside numeric summaries strengthens SEO-relevant content by emphasizing actionable insights from the score distribution.
Interpreting the distribution also informs decisions about future assessment design and instructional planning. A tight distribution around a high mean may indicate ceiling effects and suggest increasing item difficulty, whereas a bimodal distribution often reveals mixed instruction effectiveness or heterogeneous readiness levels that benefit from differentiated interventions. Regularly monitoring these distributional features turns raw test results into strategic guidance for improving learning outcomes.
How to analyze the distribution of scores on a recent test closely — step-by-step methods
Step-by-step methods
Start by gathering and cleaning the test-score dataset: export raw scores, confirm the scoring scale, remove duplicate or corrupt entries, and handle missing values. If different sections use different point scales, normalize scores (convert to percentages or z-scores) so distributions are comparable. Record basic metadata (test date, cohort, accommodations) to enable subgroup comparisons later and ensure data integrity before any analysis.
Next, compute and visualize core descriptive statistics to reveal the shape of the distribution. Calculate mean, median, mode, standard deviation, variance, percentiles (e.g., 25th, 50th, 75th) and the interquartile range (IQR); then create a histogram, boxplot, and density plot to spot skewness, multi-modality, or clustering. For a clear step-by-step:
- Plot a histogram to view overall shape.
- Overlay a density curve or kernel estimate to check for multiple peaks.
- Create a boxplot to identify IQR and clear outliers.
- Tabulate percentiles to define cut scores or proficiency bands.
Investigate outliers and subgroup differences as a focused step. Use IQR or z-score thresholds (e.g., |z|>3) to flag extreme scores, then inspect those records for data errors or valid anomalous performance. Break the data into meaningful cohorts (class, instructor, demographic groups) and rerun summaries and visualizations to detect equity gaps or instructional effects. Perform item-level analysis where possible—item difficulty and discrimination—so score distribution insights connect back to which questions drove overall patterns.
Finally, translate distribution findings into actionable metrics and reporting artifacts. Prepare annotated charts highlighting mean/median, percentile cutoffs, and any notable skew or bimodality; export tables of summary statistics and flagged outliers for stakeholder review. Document the analysis steps, thresholds used (e.g., z-score cutoff), and any normalization applied so follow-up analyses or longitudinal comparisons remain reproducible and transparent.
Visualizing the distribution of scores on a recent test closely: histograms, box plots, and density curves
Visualizing the distribution of scores on a recent test starts with choosing the right charts: histograms, box plots, and density curves each reveal different aspects of the same data. Histograms show the frequency of scores across intervals, making it easy to spot skewness, clusters, and gaps. Box plots summarize central tendency and spread with median, interquartile range (IQR), and whiskers, quickly flagging outliers and group comparisons. Density curves provide a smoothed view of the distribution that highlights modes and subtle shape features without the discretization of bins.
A histogram is ideal when you want to see how many students fall into score ranges and detect multimodality or gaps in performance. Choose bin width carefully: too wide hides structure, too narrow creates noise; using Freedman–Diaconis or Scott rules or trying several bin sizes helps find a clear picture. For SEO relevance, include terms like “bin width,” “frequency,” and “skewness” when describing how histograms reveal whether most students cluster above or below a passing threshold or whether the distribution is long-tailed.
Use a box plot when comparing distributions across sections, classes, or test versions because it compresses distributional information into a standard summary—median, IQR, whiskers, and outliers—so differences in spread and central tendency are immediately visible. Box plots are less effective at showing multimodality or exact score concentrations, so pair them with histograms or density plots when you need both summary and shape. Emphasize keywords like “outliers,” “median,” and “IQR” to help search engines match queries about score variability and anomaly detection.
Combine a density curve with histograms or box plots to balance detail and smoothness: density curves use a bandwidth parameter to control smoothing, and adjusting bandwidth reveals subtle bumps (multiple modes) or smooths over noise. Best practices include overlaying a density curve on a histogram, standardizing axes when comparing groups, and annotating key percentiles or thresholds for clarity.
Best practices
- Try multiple bin widths and bandwidths to avoid misleading artifacts.
- Overlay density curves on histograms for combined insight into frequency and shape.
- Use box plots for quick comparisons and histograms/density plots for detailed shape analysis.
Key statistics to extract from the distribution of scores on a recent test closely (mean, median, variance, skewness)
Essential statistics for analyzing test score distributions
When examining the distribution of scores on a recent test, start with the core measures of central tendency and shape: the mean, median, variance, and skewness. The mean (average) summarizes overall performance and is useful for comparing classes or test versions, but it can be pulled by extreme values. The median gives the middle score and offers a robust alternative when outliers or a non-normal distribution distort the mean, making both measures essential for accurate interpretation of test score distributions.
Variance quantifies score dispersion around the mean and, along with the standard deviation, shows how consistently students performed. High variance indicates wide differences in achievement — useful for flagging mixed mastery or uneven instruction — while low variance signals similar performance levels across the group. Reporting variance and standard deviation alongside central tendency helps educators and analysts understand both typical outcomes and the range of learner experiences.
Skewness describes asymmetry in the test score distribution and reveals whether scores cluster toward the high or low end. A right (positive) skew suggests many low scores and a few high performers, possibly pointing to a difficult exam or gaps in preparation; a left (negative) skew suggests the opposite. Interpreting skewness helps in diagnosing ceiling or floor effects, informing whether test items were too easy, too hard, or if specific subgroups need targeted support.
Used together, these key statistics create a concise, SEO-friendly profile of test performance: central tendency (mean, median), spread (variance/standard deviation), and shape (skewness). Combining them enables data-driven decisions about curriculum adjustments, item analysis, and interventions without relying on any single metric, and they form the foundation for deeper analyses such as item discrimination or subgroup comparisons.
Interpreting anomalies and turning the distribution of scores on a recent test closely into actionable insights
When a recent test’s score distribution shows unexpected patterns, educators and assessment leads must move beyond surface-level averages to diagnose anomalies and extract actionable insights. Look for skewness, unexpected gaps or clusters, and a higher-than-expected number of outliers; these signals often point to issues such as ambiguous item wording, misalignment with taught standards, or uneven student access to preparatory resources. Framing the problem with keywords like “test score distribution,” “anomaly detection,” and “assessment analysis” helps prioritize SEO visibility while guiding stakeholders toward data-driven remediation.
Start the interpretation by comparing the recent distribution to historical baselines and expected performance bands (percentiles, standard deviation). Perform item-level analysis to identify which questions drive dips or peaks: items with low discrimination or surprising difficulty shifts indicate content or instruction gaps. Cross-tabulate scores with demographics, attendance, and instructional exposure to distinguish systemic patterns from random noise—this makes the anomaly actionable rather than anecdotal.
Practical steps to convert anomalies into actions
- Flag outlier items and clusters for review by content specialists and teachers.
- Prioritize interventions by impact: focus first on frequently missed, high-stakes standards or items with wide performance variance.
- Design targeted remediation (mini-lessons, scaffolded practice, or reteach plans) tied directly to the problematic items or standards.
- Monitor short-cycle assessments and formative checks to confirm whether score distributions shift as expected after interventions.
Translate findings into classroom and program changes by assigning clear owners, timelines, and measurable success criteria for each intervention; for example, link item revisions to curriculum teams and remediation plans to grade-level teachers. Use dashboards and annotated distributions to communicate which anomalies were corrected and which require further study, ensuring decisions remain transparent and anchored in the original score-distribution evidence
Did you like this content Closely Examining the Distribution of Scores on a Recent Test: Key Insights See more here General Mechanics.

Leave a Reply